�M�^�[�̂��߂̐V���� ��؉����ɂ��� �s�^�S���X�ƃ~�[���E�g�[���̋�����K�ˍs�������Q 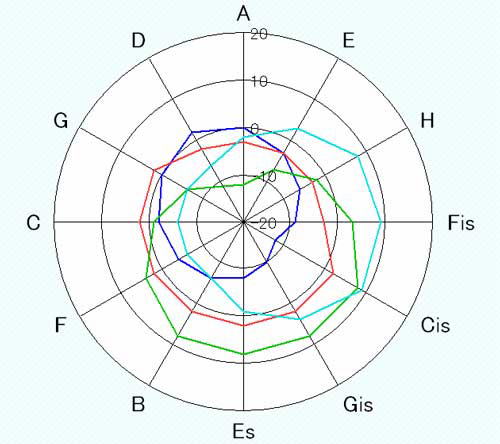 �@�@�@�@�@�@�@�@�@ ���ܓx�����[�_�[�}�� ��؉����u�ʎ�v ��؉����ɂ��ā@�@ �����v�� ��� �� �͂��߂� �M�^�[�͕��ϗ�����肩���ɂ��āA����ƂƂ��ɐ��������y�킾�Ǝ��͎v���Ă��܂��B�ł�����M�^�[�ɂƂ��āA���̋��S�n�̗ǂ������������ϗ��������ł͂Ȃ����Ƃ��ŏ��ɖ������Ă����܂��B�M�^�[�̋����ɋ��������������Ă���ɂ��S�炸�A�X�Ȃ�v�������Ă݂����Ɗ��������Ƃ́A�����ɂ���Đ��܂�鋿���ɑ��Ăł����B���ϗ��͔��ɏ����������ǂ��A�P�Q���̃n�[���j�[�Ō�����{���̂����A�T�{���������������Ȃ�������Ă��邾���ł��B�t���b�g���������M�^�[�ɂ͍œK�ȉ����ł͂���܂����A���B�̎��������ł��鋿����������Ɗ����邱�Ƃ��ۗ��ł�����A���ϗ��ɑ���v���͂R�x�����̑���̉��P�Ƃ������ƂɂȂ�܂��B ���̎��R�E�ł͑S�Ă��ψ�ł��邱�Ƃ͂قƂ�ǂȂ��A���ςƂ��������Ƃ����ԗl�͐l�Ԃ��ӎ��I�ɒP���������T�O�ł����āA���B�͗����c�݂��炬�Ƃ�������Ԃ̒��Ő����Ă��܂����A���̂��Ƃ�������p��ł���Ƃ������͊����Ă��܂��B����Ȋ��o�I�ȗv�f����ł͂���܂����A�����ɂ����̂悤�Șc�݂̗v�f�������Ă��邱�Ƃ̕������R�Ȃ̂ł͂Ȃ����Ǝv���悤�ɂȂ�܂����B�l���Ă݂�Ε��ϗ��͉����ł����āA���H�����ł͊y��i�����y��Ƃ��Ĉʒu�Â���j���K�v�ł�����A�c�݂͐���덷�⒲�����̐F�X�ȗv�f���� �������Ă��܂��̂ŁA���ꂾ���ł��c�݂͏\���Ȃ̂ł͂Ȃ����Ƃ����l����������܂��B �������A����͒P�Ȃ�����I�ȗ���ɉ߂��Ȃ����̂ł�����A ���炩�̑z�O�Ƃ��ӎu�̎Y���Ƃ��Ắu�|�v�Ɛ\���܂����A�u�@�v�Ƃł������܂����A�̌����錻�ۂƂ��ĕ\�����Ƃ��ł��Ȃ����Ƃ̎v������A�M�^�[�̉������čl���Ă݂悤�ƍl���܂����B �M�^�[�ł͍K���s�K���A�@�\��S�Ă̒����ՂȂ��g�p���邱�Ƃ͂���܂���A�g�p�p�x�̋ɒ[�ɏ��Ȃ��n�[���j�[�́A����������������Ă����H��͉e�������Ȃ��̂ł͂Ȃ����ƍl���A ���i���p����a���̋����ω����ꂽ��Ԃ���J�����A�����ł������ɋ߂Â��邱�Ƃ� ���݂邱�Ƃɂ��܂����B �����v�̖ڕW ���X�̌ÓT����������܂����A�T�ˋ��ʂ��Ă��邱�Ƃ́A�����ɏ����ɋ߂������𑽂��g�p�ł���悤�� �v���邩�Ƃ������Ƃł��B ���̍s�ׂ͕\�ʓI�ɂ́A���R�x�����̔��������ǂ̂悤�ɍ\���z�u���邩�Ƃ�������ɏI�n���Ă���悤�Ɍ����܂����A�����̔���������芴�͂���Ƃ͑S���Ⴄ�v�f�ɂ���Ďx�����Ă���ƌ����Ă悢�Ǝv���܂��B�{���A�ÓT�����̌��_�̓o�����X�̎�ꂽ�G���n�[���j�b�N�i�ٖ������j���������邱�Ƃ�����ɂ���܂�������A�Öق̂Ƃ��������R�̂Ƃ����ׂ����A�K�{�̗v���Ƃ��ĂQ�{���ł��� �I�N�^�[�u�������ȏ����ɕۂ��Ƃ���n�܂�A�����͂T�x�ƂR�x�̏��������ɂ�������Ă��܂������A���j�I�ɂ͎���ɂ����� �������邱�ƂɂȂ����o�܂�����܂��B ���̎���������������ŁA�R�{���ƂT�{���̋����ۂ��M�^�[�̋����Ɍ��ʓI�Ɏ�荞�ނ��߂ɂ́A���S�T�x�ƒ��R�x�������ǂ̂悤�ɐv���邩�Ƃ�������ɋA�����邱�ƂɂȂ�܂��B �����̌ÓT�������M�^�[�ɉ��p����ꍇ�ɖ��ƂȂ�̂́A�t���b�g�������ɑŐ݂ł��Ȃ����Ƃ����łȂ��A���̃Y�������傫�����Ƃ��ő�̓�_�ł��B�Y�����������ꍇ�̓t���b�g���Ȃ��邱�ƂőΉ����o����悤�ɂȂ�܂��̂ŁA�M�^�[�p�̉�����v����ꍇ�́A�����ȋȂ�ő傫�Ȍ��ʂނ悤�ɂ��邱�Ƃ��K�v�ł��B�M�^�[�ɂ͌��Պy��Ƃ͈قȂ���L�̏���������܂��̂ŁA�����܂�����ōœK�Ȃ��̂�I�肷�邱�Ƃ��K�v�ł��B�����őI��Ƃ������t���g�������R�́A�M�^�[�ł������Ȓ��R�x���������邱�Ƃ͉\�ł����A�s�^�S���X������~�[���E�g�[���̓����I�Șa���̋����������������͍��܂������A�M�^�[�ɓK���鉹�����ǂ����͕ʂƂ��āA ���������畽�ϗ��܂ł̉ߒ��̒��ɖ����̉�������邱�Ƃ��\������ł��B�������A���ۂɎg�p����ƂȂ�M�^�[�����ɂ�钲���̐����� �傫���Ȃ�܂��̂ŁA�Q�S���̔������炢�͐S�n�悭���t�o����悤�ȉ��������K�v������ƍl���܂��B���㉹�y�̓��}���h�������ߑ�ɂ����āA���ϗ��ɂ���Ĕ��W���ϗe���܂����̂ŁA�Ȃɂ���Ă͌ÓT�����̎g�p��f�O������܂��A�Q�O���I���y�̓����ł���u���y�̑�O���v�͌ÓT�����̎g�p�͈͂��g�債�Ă���Ƃ��l�����܂��B �����N���V�b�N���y�̐V���ȓW�]�������Ȃ����݂ɂ����āA���j����ɌJ�Ԃ��ė����悤�ɁA�ÓT�Ɋw�ѐV���Ȏ��������悤�Ƃ���s�ׂ� �Ӌ`���邱�Ƃł���Ǝ��͐M���Ă��܂��B���̂悤�ȍl������A����܂ŃM�^�[�ł͂��܂���H����ė��Ȃ������������Ɏ��g��ł݂悤�ƌ��ӂ��܂����B�����̌ÓT���������̂܂܃M�^�[�Ŏg�p�ł��Ȃ��ȏ�A�����ό`���s�Ȃ����V���ɍ��o�����Ƃ����I��������܂����A���ǂ͕ό`���x�̈Ⴂ�ł����Ċ�{�I�ɓ������Ƃł�����A���̓M�^�[�̓�����O��Ƃ����V���ȉ����Ƃ��Đv���铹��I�т܂����B�ȉ��ɂ��̉����v�̒B���ڕW�������܂��B �M�^�[�p�V�����̖ڕW �@�����������܂ނ��߂Â��邱�ƂŁA���ϗ�����������������n��o���B�@ �@���ɂR�x�����͏���(-14)�Ƃ̒���(-7)�����ǂ����������B �A�s�^�S���X�����̂R�x���������R�x�����Ȃ��B �@�܂蕽�ϗ��Ƃ̍����W�Z���g���傫���Ȃ�Ȃ����Ƃł���B �B���S�����̂T�x���������T�x�����Ȃ��B �@�܂蕽�ϗ��Ƃ̍����R�D�S�Z���g�ȏ�ɂȂ�Ȃ����Ƃł���B �C�g�p�p�x�̍����a���ɔ�����������z�u����B �@�܂蔒�����������Ƃ���a���i�_�C�A�g�j�b�N�̒��O�a���j�ɔz�u����B �D�������̕ω��͌ܓx���ɉ����Ċ��炩�ɕω�����悤�ɐݒ肷��B �@�������邱�ƂŁA���钲�����ŋ����̃o�����X���Ƃ邱�Ƃ��ł���B �E�M�^�[�Ŏg�p�\�ȃt���b�g�̃Y�����ƂȂ�悤�ɐݒ肷��B �@�M�^�[�̌����ɂ�蓖�R�ς��Ă��邪�A�W�������̂U�T�Omm�łSmm �����@��ڕW�Ƃ��Ȃ�����A �����x����������ꍇ�ł͍ō��ł��Tmm�ȓ��Ƃ���B�ȏ�̍��ڂ����ׂď[������������邱�ƂƂ��܂����B �T�x�����̈��� �܂��d�v�Ȃ��Ƃ͂T�x�����̈���ł����A���R�x�ƒZ�R�x�̐ςݏd�˂����S�T�x�ł�����A �T�x�����肵�Ȃ���� ���Z�R�x�̉������T�x���T�[�N���Ŕg�ł��ƂɂȂ�A���钲���Řa���̋����o�����X�������Ȃ�܂��B ���z�͂T�x�̉����ŏ����Ƃ̏����ȍ������A���̌��ʂƂ��ĂȂ�ׂ��傫�ȂR�x�̕ω��ݏo�����Ƃ��ł��邱�Ƃ��]�܂�邱�ƂɂȂ�܂��B ���̂悤�ȗǂ���Ƃ��ă��@���b�e�B������ �グ���܂����A���̉����͌ÓT�����̒��ł͏����ȂR�x�̋����͂Ȃ�����ǂ��A�����T�x�U�ɏ����Ɓ|�S�Z���g���i1/6�R���}���j�̂U���A�Ȃ���肵���\���ƂȂ��Ă���A���̌��ʂƂ��Ē��R�x�̋����́A�|�W�Z���g�̋������R�ŁA �|�S�Z���g���Q�A���ϗ��Ɠ����������Q�A�s�^�S���X�̂R�x���R�ƂȂ�\�������Ă��܂��B �ꌾ�Ō����u�Ȃ̂Ȃ����f�ȋ����̉����v�ł���A���ϗ��ɋ߂��ÓT�����ł���Ƃ����܂��B�i�Z���g�\���͊�{�I�ɕ��ϗ��Ƃ̍��Ƃ��ĕ\�����܂��j ����A�M�^�[�͍\���I�Ƀt���b�g�����y��ł�����A���������ȊO�ł̓t���b�g���ɑŐ݂��邱�Ƃ��ł��Ȃ��Ȃ邽�߁A�t���b�g�ʒu�̃Y�����͋ɗ͏��������Ƃ��]�܂�܂��B�o���I�ɂ͂Smm���x�ł���A�ő�ł��Tmm �ȓ������x�ł��낤���A�ӏ����ŏ����ɂ��ăt���b�g�{�[�h�̒������ɂȂ����Ƃ����҂���܂��B ���������ł́A�P�I�N�^�[�����������������������ŏ��̃R���}�Ƃ��ďd�˂邱�ƂŁA�T�x�����������ɋ߂��ݒ肵�A ���̑��̊e�������R���}�̐ςݏd�˂ɂ��ߎ����邱�Ƃɂ���ĉ������������܂��B ���̏ꍇ�͂P�I�N�^�[�u���������Ɠ������ƂȂ鉹�Q�̉����ƂȂ�܂����A�����̃t���b�g�������ł��܂��B���ϗ��͂P�Q�������ł�����t���b�g�͒����ł���A�V���ȉ������\�z����ɍۂ��ẮA���ϗ��̗l�Ɉ��肵���T�x����ՂƂ��ĉ������\������A�t���b�g�̋Ȃ�͏������Ȃ�ł��낤�Ɨ\�z�ł��܂��B �����Ɖ����̘c�� ���ɁA�ǂ̉��ɂǂ̒��x�̘c�݂���������̂��悢�����l���Ȃ���Ȃ�܂���B�����͈�ʓI�ɂ͂��ꂼ��̉��ϗ��Ƃ̃Z���g���ŕ\�����邱�Ƃ������̂ł����A����͌�������ς���A�Q�{���ł���I�N�^�[�������S�W�x�Ƃ��邽�߂ɁA���ϗ��Ƃ̃Z���g���� ���m�ɋK�肷�邱�Ƃɂق��Ȃ�܂���B�������ċK�肳�ꂽ�����ɂ�����Q�̉��̉����́A�������̃Z���g������Ⴂ���̃Z���g���������A���̉����̂Q���̉������Ƃ��ċ��߂��܂��B�����𗝉����邽�߂ɂ́A�����ȂT�x�́{�Q�ł���A�����Ȓ��R�x�́|�P�S�i���m�ɂ́|�P�R�D�U�j�ł��邱�Ƃ��o���Ă������Ƃ��K�v�ł��B���Ȃ݂ɁA�����̒Z�R�x���������S�T�x�|���R�x�ł�����A�{�Q�|�i�|�P�S�j���{�P�U�ł��邱�Ƃ͗����ł���ł��傤�B �����Ŋ�{�I�ȉ����̐����ɂ��Đ������Ă����܂��傤�B �����P�F���ꉹ���̑��a�͂O�ł��� ��̗�Ƃ��ĂT�x�����ōl����ƁA���ꂼ��̘a�����ܓx���̉E���łb���瑍�a����� �i�f�|�b�j�{�i�c�|�f�j�{�i�`�|�c�j�{�i�d�|�`�j�{�i�g�|�d�j�{�i�eis�|�g�j�{�i�bis�|�eis�j�{�i�fis�|�bis�j�{�i�ds�|�fis�j�{ �i�a�|�ds�j�{�i�e�|�a�j�{�i�b�|�e�j���O�ł��邱�Ƃ́A�S�Ẳ����{�Ɓ|�łP��Âo�Ă��邱�Ƃ��疾���ł��B ����͂ǂ�ȉ����ł������ł���A���ϗ����������̗ǂ������ƈ��������̍��v�������ƂȂ邽�߁A�ǂ�������������� �����̑������������t���Ă܂��Ƃ������Ƃł�����A�K�v�ȏ�Ɉ������������Ȃ����߂ɂ́A�T�x���ʼnE�ׂ̉��Ƃ̉������A�����ł���Q�Z���g���傫���Ȃ�Ȃ����Ƃ��K�{�̗v���ƂȂ�܂��B����Ƃ͋t�ɂT�x���������ϗ�����������ꍇ�́A���S�����̂T�x�́|�R�D�S�Z���g���L���Ȃ�Ȃ����Ƃ��v�����ƂȂ��Ă��܂��B �����Łu�����̘c�݁v�����́u�����̘c�݁v�ɂ��Đ������܂��B���̃e�L�X�g�ł́A�u�����̘c�݁v�Ƃ́u���ϗ��Ƃ̉������a�������́v�Ƃ��܂��B �܂�A�����̃Z���g���̐�Βl�̑��a�Ƃ������ƂɂȂ�܂��B�܂��A�u�����̘c�݁v�Ƃ́A�e���̂T�x�y�ђ��R�x�̉����ɂ�����Z���g���̂����A �u���ϗ���舫�����l�����v�������́v�Ƃ��ċK�肵�܂��B�܂�A�T�x�ł͕��̐��l�̍��v�ł���A���R�x�ł͂O���傫�����l�̍��v�ƂȂ�܂� �B�ǂ������ƈ��������̍��v�͂O�ł�����A�c�݂̒��x�͕��̋L������蕥���ĕ\�����邱�Ƃɂ��܂��B �T�x�ƂR�x�̐��� ������c�߂ċ����ɕω���t����ɂ́A�ܓx���ɉ����ĉ����������Âω������邱�ƂłT�x���������肳���邱�Ƃ��ł��܂��B �s�^�S���X�ł͂Q�Z���g�Â������邱�Ƃŏ�������������Ă��܂����A���S�����ł́|�R�D�S�Z���g�ÂႭ���ď����R�x��ł��܂��B �����v�̖ڕW���炷��A�T�x�̕ω��������̗��҂����x�Ƃ��邱�ƂɂȂ�A���͈̔͂łR�x�����������ǂ������ɋ߂Â���v�����邱�ƂɂȂ�܂��B �Q�Z���g���z����Ə������牓�����邾���łȂ��A�������T�x�𑽂����o�����ƂɂȂ�܂��B���@���b�e�B�������O�����������ÓT�����́A�قƂ�ǂ����̕K�{���������Đv����Ă��܂��B �����ȂT�x�͑����ق��������̂ł����A�����̈����T�x���o���邽�߁A�v�ڕW���珃�������̐�����ɂȂ邩���v�Z���܂��B �����Q�F�����T�x�͍ō��łV�ł��� �����T�x(+1.95)�̐������Ƃ��A�����T�x(-3.4)�����Ƃ���ƂP�D�X�T���|�R�D�S�����O�ł���A���{�����P�Q�ł��邩��A ���̘A���������������ƁA�����V�D�U�ƂȂ�A�����T�x�͂V�ƂȂ�B���̐��l�̒[�����グ��W�ƂȂ�A���̏ꍇ�ł��قږڕW�ɏ���������������ł��傤���A�ǂ����ŃV�������邱�Ƃ��l�����܂��B�����A�R�x�̏��������ނT�x�́|�R�D�S�Z���g�ł����A�����S�D�T�ł�����S�܂ł͎g���܂��̂ŁA���̂T�x���S�ςݏグ�邱�Ƃ� �������R�x�������o���܂����P�����ƂȂ�܂��B���̏ꍇ�͂���ȊO�̂W�������Ƃ���̂ł͂Ȃ��A���ϗ����������̗ǂ��T�x�� �ݒ肷�邱�ƂɂȂ�܂��B���Ȃ݂Ƀ��@���b�e�B�����͂����U�ŗǂ��������X�ƂȂ��Ă��āA�����������P���炵�������������T�x�̑��肪�a�炢�ł��܂����A�����R�x���������d�l�ɂȂ��Ă��܂��B�R�x�����͂T�x�����܂�ΕK�R�I�Ɍ��܂邱�Ƃł�����A�����v�͂R�x�������ǂ̂悤�ɍ\���z�u����邩�����Ȃ���A�T�x�����肷����@���ȒP�ł��B �����̘c�݃��x���ɂ��� ���̎����܂��A���@���b�e�B�����̉����̘c�݂����P���A�����T�x�i-2�j���P���炵�ĂT�ɂ��A�ǂ��T�x�i+2����+1�j���P���₵�ĂV�ɂ��邱�ƂŁA�T�x�̋�����S�̓I�ɔ�������������悤�ɐݒ肵�Ă͂ǂ����ƍl���܂����B ���@���b�e�B�����͖��ʂ��Ȃ��悭�ł����ÓT�����ł���Ǝv���܂����A�M�^�[�ł͒����I�ɑ��������Ȃ����A�M�^�[�Ŕ����������悤�ɒe���Ղ������Ɍܓx���ʼn�]���ďC�����Ă��A�t���b�g�̋Ȃ肪�傫���Ȃ��Ďg���Ȃ����߂ł��B �����Ă��̍l�����ł́A��{�I�Ƀ��@���b�e�B�����������������R�x�͍��Ȃ����ƂɂȂ�܂����A���@���b�e�B���������Ƀt���b�g�� �Ȃ肪�傫�߂��邱�Ƃ�����A��̑I�����Ƃ��Ď���邱�Ƃɂ��܂����B �������t�ɑ�����������a�炰�邱�Ƃ��ł���v���X�v�f������܂��̂ŁA���ϗ��ɋ߂��Ȃ�܂����A�o�����X�̎�ꂽ����̏��Ȃ������ƂȂ�ł��傤�B �V�����������\�z����ɂ������āA�T�x�̉����̓��@���b�e�B�Ɠ��l�ɕ��ϗ��ƂQ�Z���g�������x�Ƃ��č\�����邱�Ƃɂ���ƁA�����T�x���|�Q�~�T���|�P�O�ł�����A�ǂ��T�x���V�ɂ��悤�Ƃ���A+�Q ���R��+�P���S�Ƃ������ƂɂȂ�܂��i+2�~3�{1�~4��10�j�B�P���ɕ��ς�����ɂ��ω������Ă������̂ł����A�`���[�i�[���g�p����ꍇ�̂��ƂȂǂ��l�����āA �����ł̓Z���g�̌��͐����P�ʂōs�Ȃ����Ƃɂ��܂��B ���@���b�e�B�����̈����T�x�� �����ƌ��点�ǂ�ǂϗ��ɋ߂Â��܂��̂ŁA�������R�x�ݏo�����Ƃ��ł��Ȃ��Ȃ�܂�����A ���͍Œ���|�Q���S�ȏ�Ƃ��Đv���܂����B�ł�����T�x�̘c�݃��x���̓��@���b�e�B�����ł͂P�Q�ł����A���̕��@�ł͂P�P�`�W�܂łƂȂ�܂��B ���@���b�e�B�������������̗ǂ��R�x����邽�߂ɂ͉����̘c�݂������Ƒ傫������K�v������܂��B�Ⴆ�A�����R�x����邽�߂ɂ́|�P�S�Z���g�� �����T�x�̐ςݏグ�ō�邽�߂ɁA�Q�~�V���P�S�ł�����V�̉����K�v�ŁA��������x��t�̈����R�x�Ŗ��ߍ��킹�邱�Ƃō\���o���܂����A���̘c�݃��x���͂P�S�ƂȂ�܂��B���̂悤�ɂR�x�̏����x���ǂ�ȃ��x���ɐv���邩�ŁA�T�x�̘c�ݕ����قȂ邱�ƂɂȂ�܂��B ������v����ŏ��Ɍ��߂邱�Ƃ́A�P���ɗǂ��T�x�𑽂����邩�A�����T�x�����Ȃ����邩�Ƃ����I����������A�c��̂T�x�ς���l����������܂��B�܂�A�����T�x���V�ɂ���ƈ����T�x���T�ŁA�����T�x���S�ɂ���Ηǂ��T�x�͂W�ɂȂ�̂ŁA�ǂ����I�����邩�ł��B�܂��A �T�x�ς��Ȃ��ŏ������������邾���m�ۂ��āA�c����O�`�Q�Z���g�͈̔͂œK�x�ɒ������邱�Ƃ��\�ł��B ����̕��@�ɂ����Ă��A�T�x���V���W�P�`�Q�Z���g�ŕ��ׂĐv���邾���ŁA��؉����̓������\���I�Ɏ������ɂȂ�܂��B�����āA�_�C�A�g�j�b�N�V���ŗǂ�������ۂ��߂ɂ́A�ǂ��T�x���V�g�p����������ʂ��悭�Ȃ�̂͗e�Ղɑz���o���܂����A�����ɋ߂��R�x�ݏo�����߂ɂ́A�����T�x�����x�����ς��܂łɋ������Đ������Ȃ����邱�ƂŁA�ǂ��T�x�������Ă�����Ǖ��ɏW��������@���L���ł����A�Y��ȂR�x�͈̔͂�������Ȃ邱�Ƃ��[���ł���ł��傤�B �T�x�����̔z�u�ɂ��� ���̂T�x�����\������Ղɂ��āA�����̗ǂ����R�x�������ǂ��ɂǂ̒��x�z�u���邩�������\���̒��S�I�ȍ�ƂƂȂ�܂��B�R�x�̉����͂T�x�����̔z�u�̎d���Ō��肳��Ă��܂����Ƃ͌����܂ł��Ȃ��̂ŁA�����v�Ƃ͂ǂ̂悤�ȂT�x�̕��ו��ɂ��邩�Ƃ��� ���ł���Ƃ������Ƃ��ł��܂��B���z�I�ɂ͋ϐ��̎�ꂽ���炩�ȕω����ǂ��̂ł�����A�����悤�ȕω���A��������̂����ʓI�ŁA�M�^�[�̍\���I�ȓ��������邱�Ƃ���œK�ȕ��ѕ���ݒ肷�邱�Ƃ��K�v�ł��B ���@���b�e�B�����ł͂U�T�Omm�̌����łS�e���S�D�Wmm�A�P�e�ƂU�e���S�D�Qmm�̋Ȃ�ł����A�T�x�����E��1 �������̃����O�����ł́A�P�e�łT�D�Vmm�A�U�e�łS�D�Qmm �̋Ȃ�ł��B�V���������ł͏��Ȃ��Ƃ������� ���������邱�Ƃ��K�{�̏����ł���Ƃ�����ł��傤�B �M�^�[�̒����ł͇A�B���̊J���łf�̒��R�x�����ƂȂ��Ă��āA���̂��Ƃ��t���b�g�̋Ȃ��傫������v�f�ƂȂ��Ă��܂��B���ϗ��ł͏����Ƃ̍���14�Z���g�����邽�߁A ������ǂ����悤�Ƃ��Ă����ϗ��Ƒ傫���ς��Ă��܂��ƁA�t���b�g�̋Ȃ肪�傫���Ȃ��Ă��܂����Ƃ� ���炩�ł��B���̂��߁A�M�^�[�ł͂f�̘a���̎g�p�p�x����ύ����̂�����ǂ��܂�ۂ�ŗ}����������A�c�Ƃ`�̂Q����Ԕ����������R�x�ƂȂ�悤�ɐݒ肵�A�d�͍����O���[�v�ɋ߂����߂g�Ƒ傫���ω������邱�Ƃ��ł��Ȃ��̂ŁA�f�Ɠ����x�̉��ǂɗ��߁A�b�e�g�ϗ��ɋ߂��d�l�ō\�����邱�ƂɂȂ�܂��B �����Ŗ��ƂȂ�̂��e�̂R�x�ł����A�t���b�g�n�̓����ł�����A�ǂ����Ă������������Ȃ肪���ł��B���ϗ����x�Ƃ����Ă��ǂ��܂őË��ł��邩�ł����A���z�͂Q�Z���g�܂łł��傤���A�S�Z���g�ɂȂ�Ƒ��肪�C�ɂȂ�n�߂܂��̂ŁA�ő�������Ă��R�Z���g�܂łƂ��Ă����܂��傤�B�܂��A�f�Ƃf�����̒��R�x�������J���߂��Ă��̍����P�S�Z���g���z����ƁA��ԑ傫�ȋȂ�ƂȂ�\���̍�����P�t���b�g�̋Ȃ肪�T�������z���Ă��܂��܂��B�ł�����i�b�|�f�����j�|�i�g�|�f�j���P�S�Z���g�����x�ł��B�������K�^�ɂ��A�ǂ��T�x���V�ɂ�����@�͂��������M�^�[�̓����Ɨǂ�����ލ\���ŁA��؉����̈�ԍۂ����������ƌ����Ă悢�ł��傤�B�ǂ��T�x�̕��т̓s�^�S���X�����̓����ł���E���ɑ�������`�ł����A�t�Ɉ����T�x�̕��т͒��S�����̓����ł���E���Ō����� ���Ă����`�łR�x�̔�������������邱�Ƃ��ł��܂��B �����Ƒ���̃o�����X �����珃�������𑽂��̗p�������ƍl���Ă�����͏��n�̌��ŁA�����T�x�ɂ͂R�x�̑��肪�w���̂悤�ɂ��ĉ��܂����A�����R�x�ɂ͂T�x�̑��肪���Ă��܂��̂ō���܂��B�s�^�S���X�����������S�����̂ق����a���I�ɔ������Ɗ�����̂́A����̋����̈Ⴂ�ł��B �s�^�S���X�����̂R�x�����A���S�����̂T�x�̂ق������肪�ア����ŁA�����S�̂Ƃ��đ��肪���Ȃ����߂ł��B�P���ɕ��ϗ��ōl���Ă݂�� �A �T�x���S�ςݏd�˂�ƂR�x�ł�����A�R�x�̑���͂T�x�̂S�{�ɂȂ��ł�����A�R�x�����̑�����y������T�x�̑���͂S���̂P�Ȃ̂ŁA�����S�̂��������Ȃ�Ƃ������R�ł��B�����ŁA�����S�̂���������������邽�߂ɂ͂T�x�̏����x���������炵�āA����ł������ȋ�������������{�P�Z���g���x�ɕۂ��Ȃ���A�R�x�̑����i�K�I�Ɍ��������Ă������@���l�����܂��B ��������ς���A�ɒ[�ɉ��������̐������炷���Ƃł��B���ς��܂��Ƒ���͏������Ȃ�܂����A�t�ɑ��肪�S�̂Ɋg�����Ă��܂��������͊������Ȃ��Ȃ�܂��B�����ŏ��������Ə������Ƃ������x�����炢�ɔz�u���邱�Ƃ��ǂ��̂ł͂Ȃ����ƍl���܂����B ���̂悤�ȍl��������A�����M�^�[�p�Ƃ��čŏ��ɑI�����́A�T�x�̔��������ɒ[�ɑ��Ȃ�Ȃ��悤�Ƀ��@���b�e�B���݂́|�Q�܂łƂ��A�����T�x��Cis,Gis,Es �ɕ��ׂĒu���A�{�P�Z���g���S�����������ł��B����̓t���b�g�̋Ȃ肪�������A�R�x�̋��������@���b�e�B���݂Œ��f�ł����A �t�ɑ��肪���Ȃ��ɂ₩�ɕω����Ă���_�ŁA�������ɂ������Ȃ��v�f�������Ȃ��\���ƂȂ��Ă��܂��B����̓M�^�[����Ɠc�����l���̖����ŁuSuzuki�����v�ƌĂ��Ē����Ă�����̂ł��B �܂�A��؉����͂T�x�̕ω����s�^�S���X�����ƒ��S���������E�l�Ƃ����͈͂ɒu���A�M�^�[�̓����ɔz�����ĂR�x�̗ǂ��������n�����_�C�A�g�j�b�N���K�̘a���ɔz�u����悤�ɐv���A�i�b�g�ƃT�h�����ɕۂ��Ȃ���A�t���b�g�̋Ȃ��}���������Ƃ��č\�z�������̂ł��B �����v�̂܂Ƃ� �����܂ł̓��e���܂Ƃ߂Ă݂�ƁA�����v�ڕW��B�����邽�߂ɕK�v�ȗv�f�͎��̂悤�ɂȂ�܂��B �@���肵���T�x�Ƃ��邽�߁A�ܓx���ł̕ω����{�Q�`�|�R�D�S�Z���g�Ƃ��A�����ω��ʂ����Ԃ悤�ɂ���B �A���ϗ����ǂ��T�x���V�܂��͂W�Ƃ��A�{�Q�`�{�P���x�Ƃ���B �B�R�x�̗ǂ������͂c�`�𒆐S�Ƃ��A�f�d�𒆒��x�A�b�e�g�ϗ����x�ɐݒ肷��B�������e�͂R�Z���g�܂łƂ���B �C�����́A�i�b�|�f�����j�|�i�g�|�f�j���P�S���[�����v�Ƃ���B �ʏ�͂`�̉�����ɒ������܂��̂ŁA��؉��������̗�ɂ��܂��B ���ꂾ���̓��e�ł͖����̉��������܂����A�قȂ鉹���Ƃ��Ď��ʉ\�łȂ���ΈӖ�������܂���A ���̐��x�≟���Z�p���덷���ɓۂݍ��܂�Ă��܂��悤�ȏ����ȈႢ�͓��������Ƃ��čl����������܂���B�������A �����̒��j�����ł̓M�^�[�Ƃ����y��̏_����l�����āA���o�I�E���o�I�ɏ����ȈႢ�ł�����������͕̂ʂ̉����Ƃ��ēƗ������܂����B ���F���N�}�C�X�^�[��L�����x���K�[�̗������悤�ɁA �قȂ鉹���Ƃ��Ċ���܂Ƃ߂Đv���Ă������̂ł͂Ȃ����ƍl���A��؉����͖ڕW�������Đ��܂ꂽ�Z�퉹���Ƃ��āA�O���[�v�����Ƃ��邱�Ƃɂ��܂����B ��؉����̃t�@�~���[�\�� �����ŗ�؉����̈ꗗ��\�����ăt�@�~���[���Љ�܂��傤�B 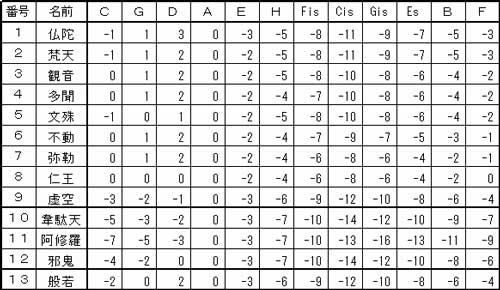 ��������ʂ��邽�߂ɖ��O��t���Ă��܂��B�P�ԁ`�V�ԂƂP�R�Ԃ͘c�݂̃��x�����قȂ��������T�̃P�[�X�ŁA�W�ԁ`�P�O�Ԃ܂ł͂����S�̃P�[�X�ł��B ���̕\�̂V�u����(�݂낭�j�v������́uSuzuki�����v�ł����A���́u���Ӂv�������w���̂ł͂Ȃ��A�����̘c�݃��x���ƍ\�����������x�̂��̂̂��Ă��āA �R�`�V�Ԃ܂ł��uSuzuki�����v�ƌĂ�ł��܂��B�ł�����\�L����ꍇ�́A���O�Ƃ��킹�āuSuzuki�����E���Ӂv�̂悤�Ɏg���Ă��܂��B�M�^�[�̉����Ƃ��Ďg�p����ꍇ�́A ��؉����̒��j���\�����Ă���A���́uSuzuki�����v���K�������̂ł���Ǝv���܂��B�T��̒��g�͒��x�̈Ⴂ�ł�����A�K���ƍl���鉹�����g�p����Ηǂ����Ǝv���܂��B �t�@�~���[�̓M�^�[�̓����ɔz���������e�ł͂�����̂́A�����̍l�����̈Ⴂ�͗e�F�������Ǝv���͈͂��L�����Đv���܂����̂ŁA �P�P�ԁu���C���i�������j�v�̂悤�� �����ڕW�̘g���������������̂������Ă��܂����A�Œ���t���b�g�̋Ȃ������Ă͂��܂����A �S�n�悭���t���邽�߂̓K���Ȓ����͈̔͂������Ȃ��Ă�����̂�����܂��B�����͖ڕW�������Đ��܂ꂽ�Z�퉹���Ƃ��āA ��؉����t�@�~���[�̈���Ƃ��Ė��𗯂߂����ƍl���ė�؉������Ƒ��\���Ƃ��܂����B ���ۂɃM�^�[�Ŏg�p����ꍇ�ɂ́A�ǂ������Ȃ�̓����������Ďg���鉹���ł����A�����ɍD�݂̖��ƒ������Ă���ł��낤�Ǝv���܂��̂ŁA�g�p�����ꍇ�͏\���Ȍ��������Ă������邱�Ƃ���]���܂��B ��Ԍ��������̂́u���C���v��u��ʓV�i�����Ă�j�v�ł��傤���A ����ł����F���N�}�C�X�^�[�� �L�����x���K�[�����ƒ����I�ȈႢ�͂�����̂́A�قړ������x�̍\���ŁA�����������悭�v����Ă��鉹���ł���Ǝ��͎v���Ă��܂��B���͂��ꂼ�����Ă͂��Ă��A ���������ł����玗�Ă��镔���������A�����\�����킩��₷�����o�������ٍ�̌ܓx�����[�_�[�}�Ō���ƁA���̌ÓT�����Ƃ̈Ⴂ�Ɨގ��_�����Ăɗ����ł���Ǝv���܂��B ���̉����́A���`�͏����_�̕t�������l�̏W���ł����A���p��̓s�����l�����Ċۂ߁A�����P�ʂ̃Z���g�l�Ŏ����Ă��܂��B ���̑��ɂ����̕\�ɍڂ�Ȃ��������Z���g�Ⴂ�̉����Q�����\�����݂��Ă��āA���ۂ̉��t�ł͌��̐��x�̖�蓙�ʼn���������A�����ȈႢ�͕��������邱�Ƃ�����ł��낤�Ǝv���܂��̂ŁA ��؉����́u�@�v�Ƃ������A�Ƃ��ĉ����̌��Ԃ߂Ă��܂��B����ł͗�؉����͂ǂ��܂ł��Ƃ����A�u�����̘c�݃��x���v�ł��b�����Ƃ���A �|�Q�Z���g���S�A�c����{�P�Z���g�ō\�������u�^�@�i����ɂ�j�v�Ƃ�����������A �u�����i�Ԃ����j�v �u�m���i�ɂ����j�v���o�āu���C���v�ɂ���Ĉ͂���͈͓��̉����ł���Ɩ����ł��܂��B �����̐����P�R����P�T�ɑ�������Ȃ�A���́u�^�@�v�Ɓu�����i��������j�v�������邱�ƂɂȂ�܂��B �u�^�@�v����؉����̂قڏ���ł���A ���́u�����v�́uSuzuki�����v�̂قڏ���Ƃ��Đv����Ă�����̂ł��B ���̃t�@�~���[�̉����ǂ����ŃA���T���u�����s�Ȃ����ꍇ�͉�������������x����܂��̂ŁA����Ȃ̓��e�ɂ���Ă͑��������Ȃ����̂�����܂����A �P�O�`�P�Q�Ԃ����������ł́A�uSuzuki�����E�����i����j�v����ɂ���ƁA���������ő�ł��Q�Z���g�ł�����A �������Q�Z���g�ȓ��œK�X����������A���̕s�ǂɂ�闐�ꂪ��������A���Ȃ��g�p�o����Ǝv���܂��B �M�^�[���y��ɂ���ĂP�{�Â�������悤�ɁA�����������Ȍ��������Ă悢�̂ł͂Ȃ��ł��傤���B ���_���M�^�[�ƌÓT�M�^�[�ł͖��炩�ɉ����̋��e�x���Ⴂ�܂����A�y��̌`��\����T�C�Y���ʼn����ɐ_�o���Ȋy����炩�Ȃ��̂�����܂��B ���������m�̏�ʼn����Ə�肭�g�����Đ��삷�邱�ƂŁA �����Ȃ�Ƃ��������������o����悤�ɂȂ�A�������t�@�~���[���������̎��݂�����邾�낤�Ǝv���Ă��܂��B ��؉����̒a���ƊW�� �����܂łɂ��b�����悤�ɁA��ԍŏ��Ɋy��Ƃ��Ċ������������́u���Ӂv�ł������A�o������r���ŐF�X�ȉ������`������A�����̊֘A�𐔗��I�ɐ������܂����̂ł����Ɍ��J���܂��B �����T�x�͂V�ƌv�Z����܂����̂ŁA����ȊO�̂T�x���v�Z���܂��ƁA�����T�x�͕��ς���ƁA�P�D�X�T�~�V���T�Ł|�Q�D�V�R�ƂȂ�܂��B �����ŏ����Ƃ��̂Q��̂T�x���������ꂼ��A�����ĕ��ׂ邱�ƂɂȂ�܂����A �M�^�[�ł̓K���Ȕz�u�́A�c�Ƃ`�ɗǂ������̂R�x������悤�ɂ��邽�߁A�����T�x���c����eis �Ƃ��܂��B���̂Ƃ��e�̂R�x�͂R�D�P�Q�Z���g�ƂȂ�A�ڕW�͂R�Z���g�ȓ��ł����A�����܂ł͋��e���邱�ƂƂ��܂��B���̉����� �u��ḎՓ��i�т邵��ȁj�v�Ɩ��t���A�P�Q���𐮐��Ɋۂ߂��������u���Ɂv�Ƃ��܂����A�S���̒[������グ����Ɓ}�̐�������Ȃ��Ȃ邽�߁A�����T�x�̔z�u���ܓx�~�Ő��Ώ̂ƂȂ�悤�ɁA�����̂d���|�Q�Z���g�ɐݒ肵�܂��B�܂��A�|�Q���c�ɐݒ肵���������u�ʎ��i�͂�ɂ�j�v�Ɩ��t���܂����A���̂Ƃ��e�̂R�x�͂S�Z���g�ƂȂ�܂��B�����̉����ł̓s�^�S���X�̂R�x���S����܂����A���ꂪ����ꂽ���̂ł��邱�Ƃ͗��j��̎����ł�����A�\�Ȍ��菭�Ȃ����邱�Ƃ����݂邱�Ƃɂ��܂��B �����R�F���R�x�̉����͂��̉�����ܓx�����E���� �S�̂T�x���������������̂ł��� �ܓx���ɂ����āA���鉹����E���ɂS�̘A�������T�x��������ƁA���̘a���̒��R�x�ƂȂ�܂��B�Ⴆ�A�b�̒��R�x�́i�f�|�b�j�{�i�c�|�f�j�{�i�`�|�c�j�{�i�d�|�`�j���d�|�b�Ƃ�����ł��B ���l�ɒZ�R�x�ł� �����S�F�Z�R�x�̉����͂��̉����܂߂� �ܓx���ō����ɂR�̂T�x�����������ĕ�����ς������̂ł��� ���̏ꍇ�́A�b�|�`���|�P�~�o�i�f�|�b�j�{�i�c�|�f�j�{�i�`�|�c�j�p�ł��B �ȏ�̐�������A�����T�x���S�A�����邱�ɂ��s�^�S���X�R�x�����܂�Ă���̂ł�����A�V�̏����T�x�̂����S�������Ɏc���ĂR���P�Z���g���Ƃ��āA�bis�`�a�ɔz�u���č\�����܂��ƁA�R�x�̉������P�Z���g�Â����ɉ��~����X�R�x�ƂȂ�܂��B ����ƂT�x�̘c�݂͂Q�~�S�{1�~�R���P�P�ƂȂ�܂�����A�����T�x�ς���ƂQ�D�Q�Z���g�ƂȂ�̂ŁA������c�`�eis �ɒu���ĉ������������������̂� �u�s���v�Ɩ��t���܂��B�����ŕ\������ꍇ�͂g���|�R�Ƃ��A���̂S���|�Q�Ƃ��܂����A�O�D�Q�Z���g�̈Ⴂ�͐l�̎��ł͔���s�\�ł�����A���̉����̖��O���u�s���v�Ƃ��܂��B ���̈����T�x�T���|�Q�Z���g�œ��ꂷ��ƂT�x�̘c�݂͂P�O�ƂȂ�A�����T�x�̐����R�Ɍ���܂����A�|�R�Z���g�������Ȃ��Ȃ舫���R�x���s�������P�Z���g�Ây������̂ŁA�t���b�g�̋Ȃ肪�������W��ȋ����̉����ƂȂ�܂��B���̉������ŏ��ɏo�������u�����i�݂낭�j�v�ł��B �t�ɁA�����T�x���T�ɑ��₵�A�����T�x���P���₵�Ăd�ɔz�u����ƁA�c�݂��P�Q�ƂȂ胔�@���b�e�B�������O�����Ɠ����ł����A�R�x�������|�P�O�Z���g�ɂȂ�u�ω��v�Ɩ��t���܂��B�|�R�Z���g�̂T�x�������T�x���炵�Ăd����eis�Ɉړ��������̂��u�����i������j�v�ł���A �����T�x���U�ɘA�����������̂��u���V�i�ڂ�Ă�j�v�ł��B �������ČX����R�x����������āu���Ɂv�ɂȂ��邱�ƂɂȂ�܂��B�u�ω��v�Ɓu�����v�ł͂T�x�̘c�݂������ł� �R�x�̏����x���قȂ��Ă��邱�Ƃ��������̂ŁA�X�Ɍ������ǂ��Ȃ���@���l���Ă݂܂����B�u�ω��v�͔������Ǝv���܂����A�����R�x�̋������s�^�S���X�R�x������ł��낤�낵�Ă���̂����ǂ��������߁A�u�s���v�̂悤�ȌX�Ώ�ۂ��Ȃ���ǂ��R�x���������悤�Ǝ��݂܂����B���̌��ʁA�u�ω��v�̂b�AG�A�c���P�Z���g�ÂႭ���邱�ƂŁA�u�ω��v�Ɓu�s���v�̗ǂ����������d�l�ƂȂ�A ������u�����i����j�v�Ɩ��t���܂����B �������āA�u��؉����v�Őv�ڕW��B�������P�`�V�Ԃ܂ł̉������a�����܂������A���������o�I�Ɍܓx�����[�_�[�}�ŘA���\�����Ă݂�ƁA���ϗ�����u���Ɂv�� ���鉹���̕ω����������̂悤�ɕϗe���Ă����l�q�������܂��B���̏��Ԃ́u���Ӂv�u�s���v�u�����v�u�ω��v�u����v�u���V�v�u���Ɂv�ł��B ��؉����̓��� ��؉������ꌾ�ŕ\������Ȃ�A�s�^�S���X�����ƒ��S�����̊Ԃ�K�˕�����������悤�ȉ����Q�ł��B�������Ƃ����j�̒��ʼni���g�p���ꂽ���т̂��鉹���ł���A���ƌ����Ă������������x�[�X�ɍ\�z����Ă���Ƃ����_�ŁA���ɈӋ`�[�������ł��B��؉����̒��łْ͈[�ɑ�����P�O�`�P�Q�Ԃ́A�����R�x�����߂Ȃ���ڕW�̑S�Ă��N���A�[�o���Ȃ����������ŁA���̌��͊����̌ÓT�����Ɣ�r���Ă������Č���肵�Ȃ��ł��낤�Ǝv���̂ł����A�e�̋��������ЂƂƂ������ƂœK�����钲�������P�`���T���x�ɂȂ��Ă��āA�s�^�S���X�����ƒ��S�����̋����������Ă��܂��B �u����v�͂������ӎ����Ȃ��珃�����痣��ĖڕW�Ɍ������ēw�͂����A�uSuzuki�����v�̉����ƂȂ��Ă��� �u����v����Q�Z���g�ȓ��ɂ܂łɋ߂Â��Ă��܂��B�����āu�m���v�͕��ϗ��Ƃ̊Ԃɐm���������āA��؉���������Ă��܂��B�P�R�Ԃ́u�ʎ�v�́A�ڕW��B�����邽�߂̗���̌����邽�߂ɑ��݂��Ă��āA��؉����̓����������Ŏ������Ƃ��o������e���ƍl���Ă��܂��B ���݂ł͌ÓT���������ۂɎg�p�����@��͂قƂ�ǂȂ��Ȃ��Ă��܂��܂����̂ŁA���������X�M�^�[�ōČ����Ă����̈Ӌ`���Ȃ��Ǝv�����Ƃł��傤�B�������A���X�̌ÓT�������s�^�S���X�����ƒ��S���������ǂ��邱�ƂŐ��܂ꂽ���Ƃ��l����ƁA���ϗ��Ɋ���߂��Ă��܂�������̉��y�A���ɕ��ϗ�����肩���Ƃ��Đ��������W���Ă����M�^�[�̋����ɁA�Â��ǂ�����̃n�[���j�[�������Ă݂鎎�݂��A����Ȃ�ɈӖ������邾�낤�Ǝv���Ă��܂��B �����̘c�݂��������u���Ӂv���́A����̉��y�Ɏg�p���Ă�������x�̐��ʂ͓����邾�낤�Ǝv���܂����A�����̐����͂�����̂́A �����̉��ꂩ���C�ɓ���A���ϗ����g�������Ȃ��Ȃ�l�������邩���m��܂���B �����ŁA��؉����́u����E�v�Ɓu�����E�v���ܓx�����[�_�[�}�ŕ\�����āA�����͈͂����o�I�Ɏ����܂��B�F�t�����������������̊܂܂��͈͂ł���A�����E�́u���C���v�ł����A���̃G���A�ł���ΑS�ė�؉����Ƃ������Ƃł͂���܂���B�����ē��R�̂��ƂȂ���A�uSzuki�����v�́u��؉����v�͈̔͂Ɋ��S�Ɋ܂܂�܂��B ��؉����͈̔� 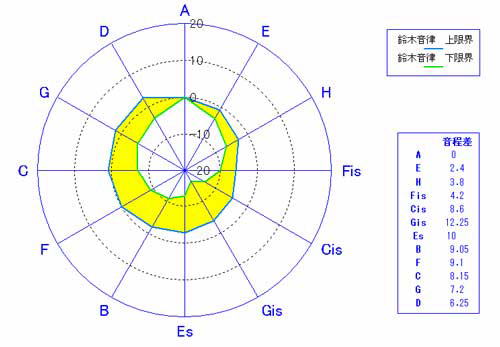 Suzuki�����͈̔͂Ɣ@ �uSuzuki�����v�͈͕̔��͂`�̗אڂ��P�Z���g�A����ȊO�͂Q�Z���g�ƂȂ��Ă��āA���̐}�̂悤�ɂȂ��Ă��܂��B���͈̔͂̉����ł���A�v�ڕW�����Ă������A�e�����ǂ�Ȑ��l������Ă��uSuzuki�����v�ł��B �M�^�[�͌��Պy��ƈ���ĐF�X�ȗv�f�ɂ���ėl�X�ɉ������ӂ���܂����A�����ł̃t���b�g�Ő덷���}�P�Z���g���x�ł��邱�Ƃ��l�����āA ���̒��x�̕��ő�炩�ɋK�肵�Ă����ėǂ��̂ł͂Ȃ����Ǝv���܂��B�������A����덷�͋���������̂ł����A�S�Ẳ��ɂP�Z���g���x�̌덷������킯�ł͂���܂���A�������ɐ��삵�����ŏ����Â������ς��Ă��܂��̂ŁA�͂��ȈႢ�ł����Ă��قȂ鉹���Ƃ��Ė��m�ɂ��Ă��������ƍl���A���O��t���Đ������Ă��܂��B ����͏ڍׂɉ��������������ۂɎ��삵�Ă݂āA�ǂ̒��x���M�^�[�ɂƂ��ēK�������ɂ߂邽�߂Ɏ�������@�ł��B Suzuki�����͈̔� 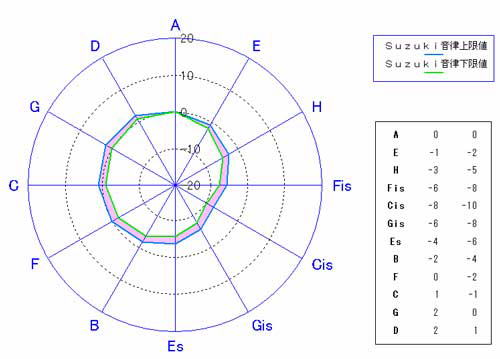 ���͈̔͂̏�����u�ٓV�v�ŁA���S���ƂȂ�̂��u�s���v�ŁA�������u����v�ł��B�ł�����A������������ɍi��ƌ�����A �uSuzuki�����v�́u�s���v�ł���Ƃ������ƂɂȂ�ł��傤�B���H��ł́u�ٓV�v���u����v���u�s���v�Ƃ̈Ⴂ���قƂ�Ǖ��������邱�Ƃ��ł��Ȃ����낤�Ǝv���܂��B ���̗��R�́A�u�s���v������ۂɂP�Z���g�グ��u�ٓV�v�ƁA������u����v�Ɨ��_��͂P�Q���̂����̂Q�����P�Z���g�Ⴄ�����̉����ɂȂ邩��ł��B ����ł͕ʂ̉����Ƃ��čl����͖̂���������悤�Ɏv���܂����A�����ĕʂ̉����Ƃ������R�͓����܂��B���͋Ȃ�̒��x���قȂ��Ă��܂��̂ŁA���삷���ł̌덷������܂����特���������Ɉ���Ă��邱�Ƃł��B��������ʂ���ۂɂ͂Q�Z���g�̈Ⴂ�͌����ď����ȍ��ł͂Ȃ��̂ł��B���͑O�f�̉����t�@�~���[�Ɍf�����Ă͂��Ȃ��A�̉����Łu��u��v�Ɓu����Ɂv���u�ω��v�Ɣ�r����ƁA�㉺1�Z���g���Őv����Ă��āA�u�s���v�̏ꍇ�����X�ɂP�Z���g���x���ϗ����牓������A�����x����������������\������Ă��܂��̂ŁA���̃O���[�v�Ƌ�ʂ��邽�߂ł��B �u����v�́u�ω��v�Ɓu����Ɂv�̂P�Z���g���̃G���A�ɓ����Ă��܂��̂ŁA�uSuzuki�����v�Ƃ͏����قȂ�O���[�v���u��؉����v�̒��ɏd�Ȃ��đ��݂��Ă��邩��ŁA�u�ω��v���u��؉����v���\���鉹���̈�ł��B����Ɠ��������ł́A�u���Ɂv�u���V�v�u�ʎ�v�����������Ƃ����܂��B�����āu����v�́u��؉����v �̖ڕW��B���������K�ȉ����Q�̑S�̎��ɂ��Ȃ��Ă��āA���̕��́}�Q�Z���g�ł�����A�ڕW�B���̋��ɂ́u����v�Ƃ������܂��B ���Ȃ݂ɁA�uSuzuki�����v�͈̔͂Ɋ܂܂�鉹���̃p�^�[���́A�����ŕ\���Ă�78732���邱�ƂɂȂ�܂��B���̑S�Ă��uSuzuki�����v�ł͂���܂��A�����邻�́u�@�v�̒�����T�̉��������\�Ɍ��J���Ă����܂��B���̂܂܍��t���Ă����͂Ȃ��ł��傤�B 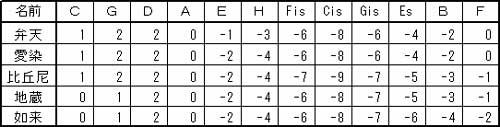 �u�����v�́uSuzuki�����v�̏���Ƃ��Ĕ��z���܂������A���̉����������O�������ܓx���Ł��P�E�ɉ����̂Ƌߎ����Ă��āA�b�łP�Z���g�A�f�łQ�Z���g�Ⴄ�����ł��B�u�ٓV�v�́u�����v�����₷���悤�ɂd�Ƃg���P�Z���g���ϗ��ɋ߂Â������̂ł����A�uSuzuki�����v�̏�����̂��̂ƂȂ��Ă��āA�u�n���v�Ƃ��R�x�̍\�������悭���Ă���z�u�ƂȂ��Ă��܂��B�u�n���v�́u���Ӂv�Ǝ��́u�@���v�̒��Ԃɂ���A�u�@���v�͉����̒��łR�x�ƂT�x�̋��������Ώ̂̌`�����Ă��āA�M�^�[�̓����ɉe�����ꂸ�ɐv����܂����̂ŁA�Ȃ肪���Ȃ��������������������ł��B�u��u���i�т��Ɂj�v�͂T�x�̘c�݂͂P�P�ł����A�f�̂R�x�̏����x���|�U�łfis���W�ƂȂ�A�����P�S�Z���g�ł��̂łP�e�̋Ȃ肪�ő���x�ɂȂ��Ă��܂��B�����āu�ٓV�v�Ɓu�s���v�͈͓̔��Ɉʒu���A�u����v���u�ω��v�Ɓu����Ɂv�̊Ԃɂ���̂Ƃقړ����W�ł�����A���h�ȁuSuzuki�����v�̈���ł��B�����ɂ͂T�x�̘c�݃��x���P�O�ɂ�����u�@�v����ɏЉ�܂����B �T�x�̘c�݃��x�������������͂R�x�̏����x�������Ȃ�܂����A����ȏ�f�o���Ă��ی�������܂���̂ŁA�����̏Љ�͂��̒��x�ɗ��߂邱�Ƃɂ��܂��B �����ɏЉ�������͐v�ڕW�Ƃ����uSuzuki�����v�̈ꕔ�ł����A���̒��x�̈Ⴂ�͓��������Ƃ��ė���������������̂悤�ȋC�����܂��B ���������̂̓M�^�[�p�̉����Ƃ��Ăǂ̒��x���K����������߂邽�߂̎��s����̌��ʂł��B�S�Ẳ��������삵�����邱�Ƃ͔�p�Ǝ��Ԃ�������܂��̂ŁA��芸�������̗\�������ɐ��삵���Q�{�̃M�^�[�̌��ʂ���A�m�M�Č��\���邱�Ƃɂ������̂ł���A�S�e�͊m�F���Ă��Ȃ����Ƃ��������Ă����܂��B�Ō�ɁA���@���b�e�B�����Ƃr���������������i���Ӂj���ܓx�����[�_�[�}�Ŕ�ׂāu��؉����v�̊T�v�Љ���I���܂��B 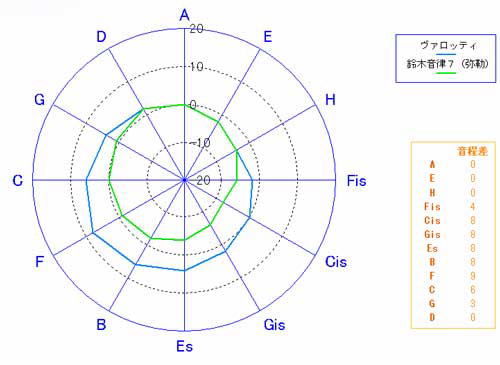 �Q�l�F�y�ܓx�����[�_�[�}�z   |